In artificial intelligence, algorithms are the backbone of intelligent decision-making. One such algorithm that has stood the test of time is Minimax AI. But what exactly is Minimax AI, and why does it matter in today’s tech landscape? Let’s dive deep into this fascinating world of strategic AI.
The Essence of Minimax AI: Strategy at Its Core
Imagine you’re playing chess against a computer. Every move you make, the computer seems to have a perfect counter. That’s Minimax AI in action. At its heart, Minimax is a decision-making algorithm designed for two-player games. It’s all about making the best move while assuming your opponent will do the same.
Key Takeaway:
Minimax AI is like a digital strategist, always thinking several steps ahead in a game or decision-making process.
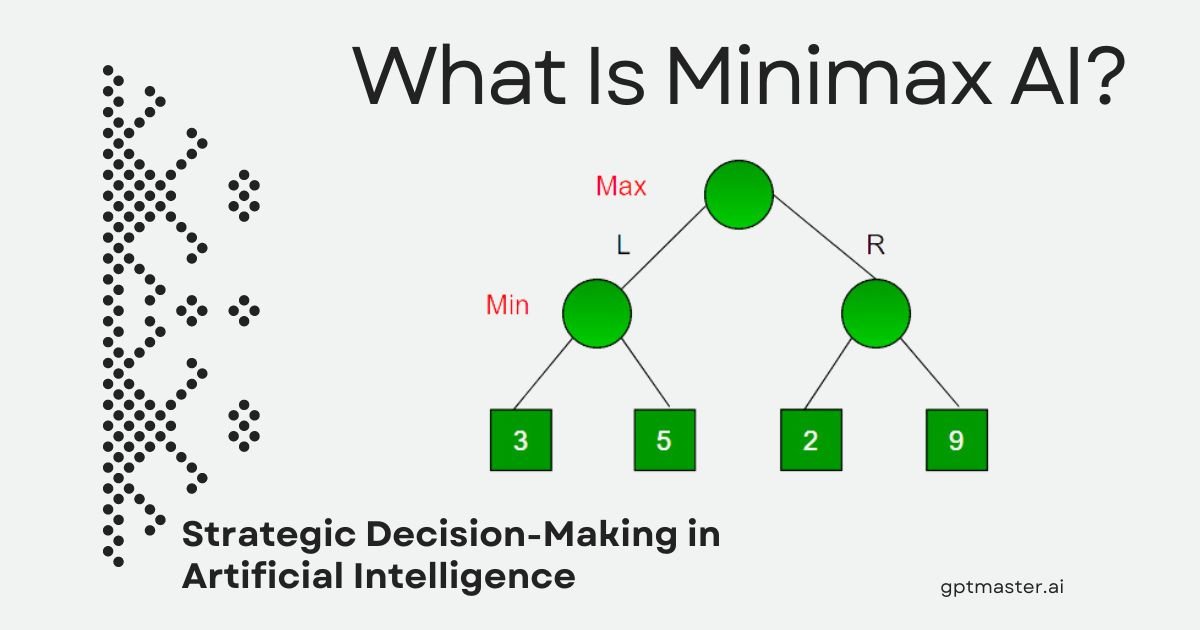
How Minimax AI Works: The Battle of Max and Min
To understand Minimax, think of it as a tug-of-war between two players: Max and Min.
- Max (usually you or the AI) tries to maximize the score.
- Min (your opponent) aims to minimize your score.
The algorithm plays out every possible move and counter-move, assigning scores to each outcome. It then chooses the path that leads to the best possible score, assuming the opponent plays perfectly.
Breaking It Down:
- Look Ahead: The AI considers all possible moves.
- Evaluate: It assigns scores to each final position.
- Work Backwards: Starting from the end, it determines the best move at each step.
- Choose: It picks the move that leads to the best outcome.
The Game Tree: Mapping Out Possibilities
Imagine a tree where each branch is a possible move. This is the game tree, and it’s crucial to understanding Minimax.
Start
/ | \
A B C
/|\ /|\ /|\
... ... ...Each level alternates between Max and Min, representing turns in the game. The deeper the tree, the further ahead the AI looks.
Pro Tip:
The depth of the game tree directly affects the AI’s skill level. Deeper trees mean smarter AI, but also require more processing power.
Scoring: The Heart of Decision-Making
How does Minimax decide what’s a good or bad move? It all comes down to scoring. Each end position (leaf node in the tree) gets a score. For example, in chess:
- Checkmate in your favor: +1000
- Losing a pawn: -1
- Neutral position: 0
The AI then works backwards, choosing the maximum score when it’s Max’s turn and the minimum score when it’s Min’s turn.
Real-World Applications: Beyond Gaming
While Minimax shines in games, its applications extend far beyond:
- Finance: Predicting market movements and optimizing trading strategies.
- Robotics: Path planning for robots in competitive environments.
- Resource Allocation: Optimizing distribution in scenarios with competing interests.
- Cybersecurity: Modeling attacker-defender scenarios to enhance security protocols.
Case Study:
In 1997, IBM’s Deep Blue used a variation of Minimax to defeat world chess champion Garry Kasparov, marking a milestone in AI history.
The Limitations: When Minimax Falls Short
Like all algorithms, Minimax has its weak points:
- Computational Intensity: For complex games, the number of possibilities can be astronomical.
- Perfect Play Assumption: It assumes the opponent always makes the best move, which isn’t always true in real-life scenarios.
- Depth Limitation: Practical implementations often limit the search depth, potentially missing long-term strategies.
Enhancements: Making Minimax Smarter
To address these limitations, AI researchers have developed several enhancements:
Alpha-Beta Pruning:
This technique cuts off branches of the game tree that don’t need to be explored, significantly reducing computation time.
Heuristic Evaluation:
Instead of calculating every possible outcome, heuristics provide educated guesses about the value of non-terminal positions.
Machine Learning Integration:
Modern AI systems combine Minimax with machine learning techniques to improve decision-making and adapt to different playing styles.
Implementing Minimax: A Simple Python Example
Let’s look at a basic implementation of Minimax for a simple game like Tic-Tac-Toe:
def minimax(board, depth, is_maximizing):
if check_win(board, 'X'):
return 1
if check_win(board, 'O'):
return -1
if is_board_full(board):
return 0
if is_maximizing:
best_score = -float('inf')
for move in available_moves(board):
board[move] = 'X'
score = minimax(board, depth + 1, False)
board[move] = ' '
best_score = max(score, best_score)
return best_score
else:
best_score = float('inf')
for move in available_moves(board):
board[move] = 'O'
score = minimax(board, depth + 1, True)
board[move] = ' '
best_score = min(score, best_score)
return best_score
def find_best_move(board):
best_score = -float('inf')
best_move = None
for move in available_moves(board):
board[move] = 'X'
score = minimax(board, 0, False)
board[move] = ' '
if score > best_score:
best_score = score
best_move = move
return best_moveThis code demonstrates the recursive nature of Minimax, evaluating each possible move and its consequences.
The Future of Minimax AI: Evolving Strategies
As AI continues to advance, Minimax remains a fundamental concept, evolving with new technologies:
- Quantum Computing: Promises to handle larger game trees, making Minimax even more powerful.
- Reinforcement Learning: Combines with Minimax to create more adaptive and human-like AI opponents.
- Explainable AI: Efforts to make Minimax decisions more transparent and understandable to humans.
Conclusion: The Strategic Core of AI
Minimax AI stands as a testament to the power of strategic thinking in artificial intelligence. From its roots in simple game-playing to its applications in complex decision-making scenarios, Minimax continues to be a crucial algorithm in the AI toolkit.
As we’ve seen, understanding Minimax opens doors to grasping more complex AI concepts. Whether you’re a developer, a business strategist, or just an AI enthusiast, the principles of Minimax offer valuable insights into how machines make decisions in competitive environments.
Remember, in the world of AI, sometimes the best offense is a good defense – and that’s exactly what Minimax AI is all about.